|
Stratified motion estimation
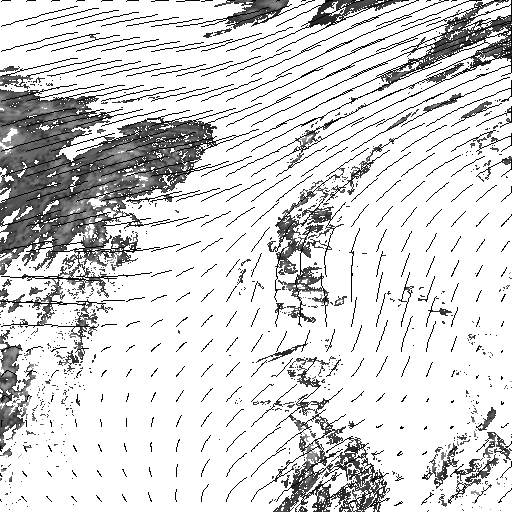
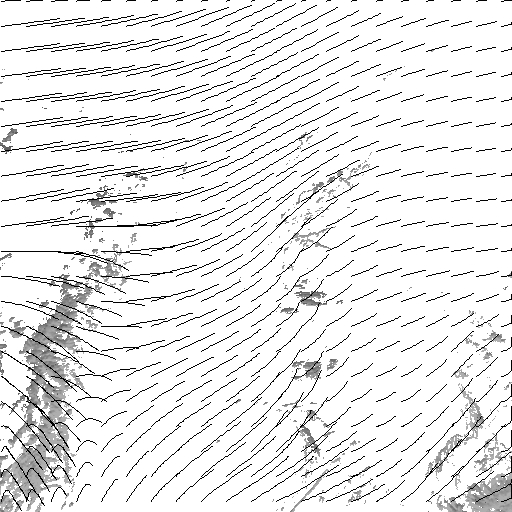
Estimating the evolving vertical distribution of horizontal wind fields from satellite image time series is of great importance for the study of atmospheric dynamics. Because of the sparse 3-dimensional nature of observations, classical correlation-based techniques are not suited for the dense estimation of layer motion. We propose a sound energy-based estimator producing dense motion fields related to the different layers in a stratified atmosphere from an image sequence. The energy function to be minimized is composed of a data term based on the integrated continuity equation and of a div-curl regularizer. Layer-related transmittance images derived from top of cloud pressure constitute the imput images. Moreover, a masking procedure together with the use of robust penalty functions on the data term allows to discard implicitly the influence of undesirable layers from the estimation process. It is important to outline that the method always provides motion vector for all points of the image domain and areas with hidden or lacking clouds correspond to interpolated wind fields.
Spatio-temporal
consistency To preserve the temporal consistency of the estimates, the variational method is temporally regularized according to a vorticity-divergence formulation of shallow water equations. The Helmoltz decomposition is employed to recover the predicted velocity field from the propagated curl and divergence components.
Results
In order to analyze
the accuracy of the estimation method, the trajectories of uniformly
spread points have been reconstructed using a fourth-order Runge-Kutta
integration method. This image sequence has been provided by the Laboratoire
de Météorologie Dynamique (LMD)
du CNRS.
References
|