|
Description Optical-flow methods dedicated to fluid motion have been recently introduced.
These approaches have the main advantage to produce dense motion fields.
However, as the underlying optimization are based on gradient descent
techniques, the estimates are very sensitive to the initialization procedure.
In particular, large displacement can only be recovered using a multiresolution
strategy with the possible drawback of smoothing out small structure
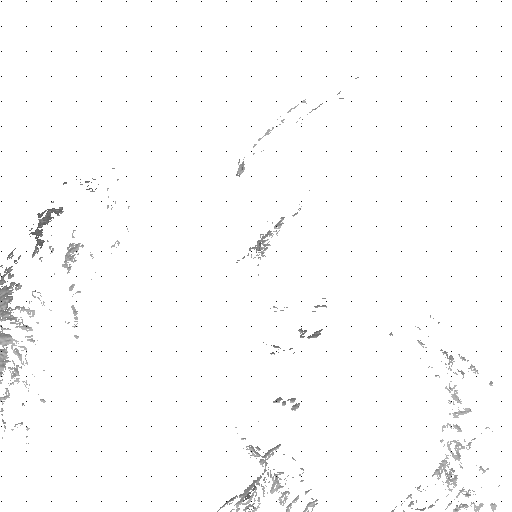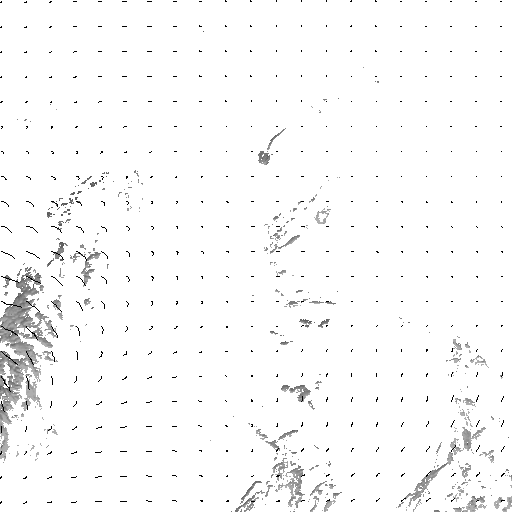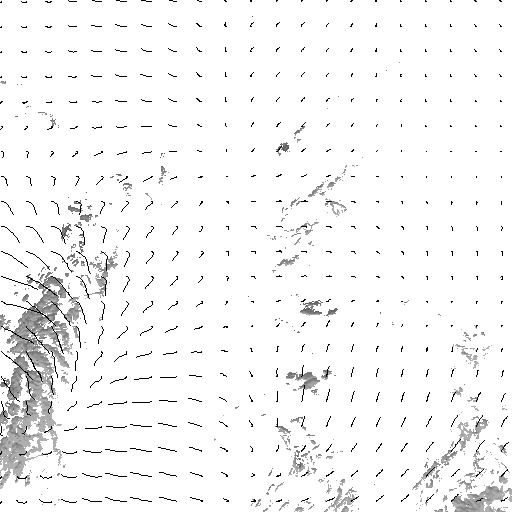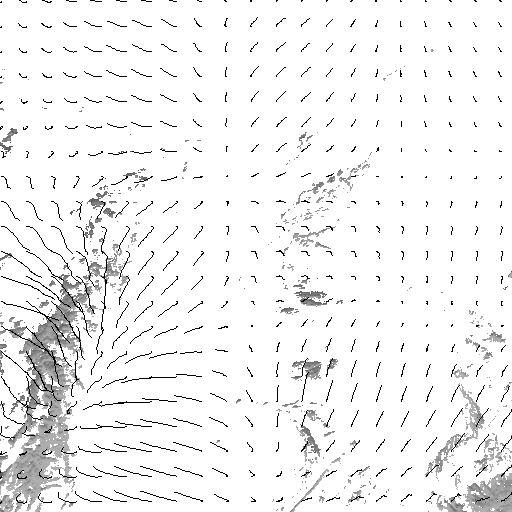
motions. To overcome the limitation induced by both optical-flow and correlation based methods, we propose to introduce an initialization scheme for a fluid dedicated dense motion estimation where the multiresolution scheme has been removed. The initial velocity field is estimated by minimization of a energy function composed of a 'div-curl' regularization and a data term. The latter constrains the dense estimated field to fit the sparse correlation vectors convoluted by bidimensional gaussian functions. The resulting vector field is then used to initialize the finest resolution of the fluid dedicated dense motion estimator introduced by [Corpetti et al., 2002]. Results
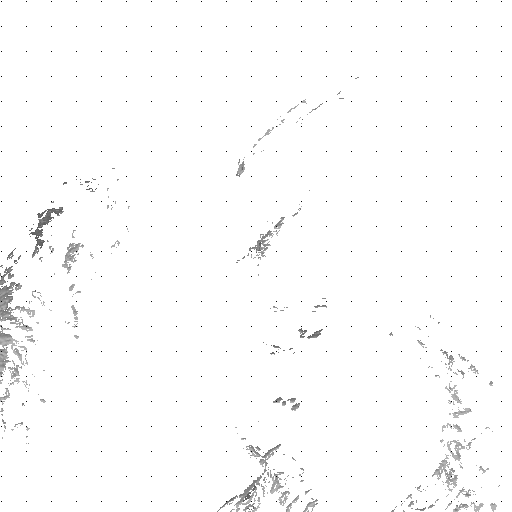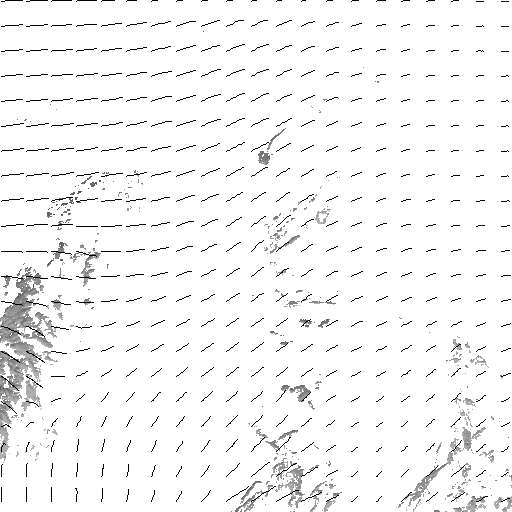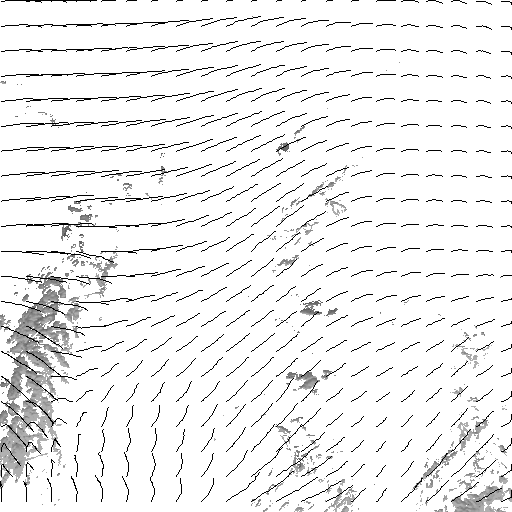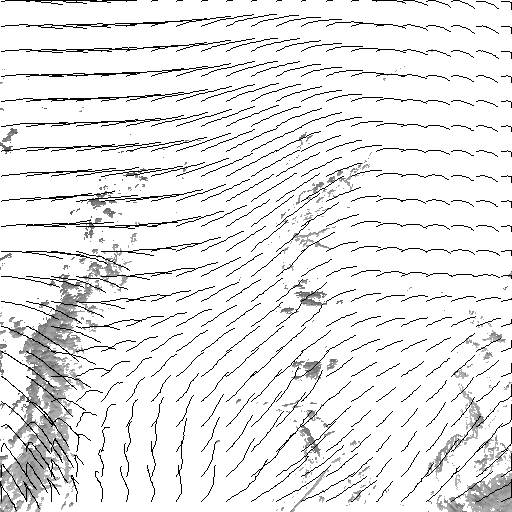
In order to analyze
visually the accuracy of the estimation
method, the trajectories of uniformly spread points have been reconstructed
using a fourth-order Runge-Kutta integration method. The following image sequence
has been provided by the Laboratoire de Météorologie
Dynamique (LMD) du CNRS.
References
|